🌞 SQL 튜닝
지난 시간에는 조인의 3가지 원리 중 하나인 Nested Loop 조인 (이하 NL 조인)에 대해서 알아보았다. 우리가 일반적으로 사용하는 이중 포문의 형태가 바로 NL 조인이며, NL 특징으로는 먼저 액세스 한 OUTER 테이블의 로우를 차례 차례 스캔을 하면서 Inner 테이블에 랜덤 엑세스하며, 부분 범위 처리에 효과적인 것 까지 알아보았다. 이번 시간에는 그 다음 차례인 Merge 조인에 대해서 알아보는 시간을 가져보도록 하자.
마찬가지로 이번 시간에도 Northwind 데이터베이스를 사용하는 것이 아닌, BaseballData 데이터베이스를 사용한다.
🐋 머지 조인
Merge(병합) 조인은 일반적으로 Sort Merge(정렬 병합) 조인이라고 한다. 이전 시간에 살펴본 SELECT 문을 통해 머지 조인은 어떤 실행계획을 가지는지 확인해보자.
USE BaseballData;
-- 지난 시간에 확인했던 MERGE JOIN
SELECT *
FROM players AS p
INNER JOIN salaries AS s
ON p.playerID = s.playerID;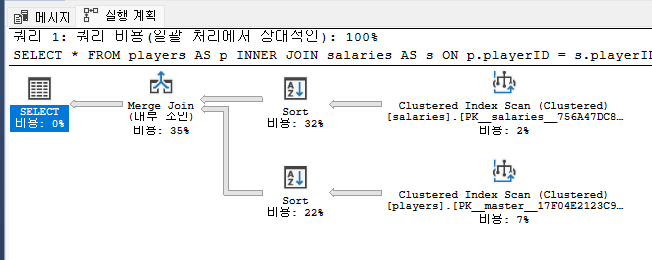
실행 계획을 보면 salaries와, players 각각에 클러스터드 인덱스가 뜨고, 이를 소팅한다. 이 후 소팅한 결과를 머지 조인하는 걸 알 수 있다. 그렇다면 원리는 어떻게 되는걸까? 오늘도 저번시간과 마찬가지로 C#을 통해 알아보도록 하자.
먼저 지난 시간과 동일하게 Player 클래스와 Salary 클래스를 구현하고, playerId를 넣어주도록 하자. 이번 시간에는 정렬이 필요하므로 IComparable을 통해 CompareTo를 구현해야하므로 해당 함수도 아래와 같이 작성하도록 하자.
class Player : IComparable<Player>
{
public int playerId;
public int CompareTo(Player other)
{
if (playerId == other.playerId)
return 0;
return (playerId > other.playerId) ? 1 : -1;
}
}
class Salary : IComparable<Salary>
{
public int playerId;
public int CompareTo(Salary other)
{
if (playerId == other.playerId)
return 0;
return (playerId > other.playerId) ? 1 : -1;
}
}
이 후, players 테이블과 salaries 테이블을 만들어 임의로 특정 데이터를 넣어주도록 하자.
static void Main(string[] args)
{
List<Player> players = new List<Player>();
players.Add(new Player() { playerId = 0 });
players.Add(new Player() { playerId = 9 });
players.Add(new Player() { playerId = 1 });
players.Add(new Player() { playerId = 3 });
players.Add(new Player() { playerId = 4 });
List<Salary> salaries = new List<Salary>();
salaries.Add(new Salary() { playerId = 0 });
salaries.Add(new Salary() { playerId = 5 });
salaries.Add(new Salary() { playerId = 0 });
salaries.Add(new Salary() { playerId = 2 });
salaries.Add(new Salary() { playerId = 9 });
}
먼저 1단계로 해야할 것은 Sorting 즉, 정렬을 하는 단계가 필요하다.
// 1단계) Sort (이미 정렬되어 있으면 Skip)
// O(nlogn)
players.Sort();
salaries.Sort();
단, 이미 정렬되어 있을 경우 해당 로직은 Skip되며, 시간 복답도는 O(n log n)을 가진다. 이 후 2단계로 해야할 것은 정렬된 데이터를 병합하는 것이다. (Merge)
// One-To-Many (players는 중복이 없다.)
// 어떤식으로 합쳐줘야 할까?
// players(outer) - [ 0, 1, 3, 4, 9 ] → N
// salareis(inner) - [ 0, 0, 2, 5, 9 ] → M
먼저 현재 조건을 One-To-Many라는 조건으로 가정하여 구현해보도록 하자. 이 말은 즉, players에는 중복된 데이터가 없다는 뜻이라는 것이다. NL 조인은 동작방식은 모든 데이터를 하나하나 다 순회하는 방식으로 진행되었지만, 머지 조인은 그렇지 않다. 그러나 머지 조인의 동작방식에 대해서 설명하면 너무 길어지므로 아래 링크로 대체한다.
* 머지 조인의 동작 방식
https://bertwagner.com/posts/visualizing-merge-join-internals-and-understanding-their-implications/
Visualizing Merge Join Internals And Understanding Their Implications
This post is part 2 in a series about physical join operators (be sure to check out part 1 - nested loops joins, and part 3 - hash match joins). Watch this week's video on YouTube Merge joins are theoretically the fastest* physical join operators available
bertwagner.com
위 링크에서 머지 조인의 동작 방식을 이해했으면, 이제 이를 의사코드로 구현해보자.
int p = 0;
int s = 0;
// Merge Sort 의사코드 구현
// O(N+M)
List<int> result = new List<int>();
while (p < players.Count && s < salaries.Count)
{
if (players[p].playerId == salaries[s].playerId)
{
Console.WriteLine($"playerId: {players[p].playerId}");
result.Add(players[p].playerId); // 성공!
s++;
}
else if (players[p].playerId < salaries[s].playerId)
{
p++;
}
else
{
s++;
}
}
먼저 결과물을 저장할 result 리스트를 만들고, 위 링크에서 봤던 것처럼 각각의 리스트에서 playerId 데이터를 비교하며 인덱스를 늘려나가준다. 만약 같을 경우 result 결과물 리스트에 저장한다. 이를 실행해보면 result 리스트에는 0, 0, 9라는 값이 들어간다. 그리고 해당 로직의 시간 복잡도는 players, salaries의 테이블 크기만큼 순회하면 되기 때문에 O(N+M)의 복잡도를 가진다.
그렇다면 이번에는 Many-To-Many일 경우 어떻게 구현해야 할까?
// Many-To-Many (players는 중복이 있다.)
// outer - [ 0, 0, 0, 0, 0 ] → N
// inner - [ 0, 0, 0, 0, 0 ] → M
// O(N * M)
// 물론 그렇다고 Many-To-Mnay가 나쁜 것은 아니지만 위 예는 최악중의 최악인 상황임.
위와 같이 아우터가 모두 0이고, 이너도 모두 0일 경우 이전의 NL 조인과 같이 모든 경우의 수를 비교해야 하기 때문에 시간 복잡도는 O(N * M)의 값을 가진다. 주석으로도 알다 싶이 Many-To-Mnay가 나쁜 것은 아니지만 위 예시는 최악중의 최악인 상황이다. 이제 다시 SQL로 돌아가도록 하자.
먼저 분석을 위해 STATISTICS 삼총사를 켜주도록 하자. 이 후 언제나 그랬듯이 클러스터드와 논클러스터드의 테이블을 대략적으로 그리고 이해를 위해 힙 테이블까지 그려주도록 하자.
-- 분석을 위한 삼총사
SET STATISTICS TIME ON;
SET STATISTICS IO ON;
SET STATISTICS PROFILE ON;
-- 논클러스터드
-- 1
-- 2 3 4
-- 클러스터드
-- 1
-- 2 3 4
-- Heap Table [ {Page}, {Page} ]
이제 진짜로 SELECT 문을 실행하여 머지조인에 대해서 알아보도록 하자.
-- 데이터 조회
SELECT *
FROM players AS p
INNER JOIN salaries AS s
ON p.playerID = s.playerID;
실행 계획을 보면 머지 조인을 하는데 Many-To-Many 즉 다대다를 통해 현재 실행이 되는 것을 알 수 있고, 둘 다 소팅을 해줘야 하는 것 까지 알 수 있다. 그렇다면 혹시 데이터가 정렬이 안 된 것일까? players와 salaries 테이블을 각각 살펴보자.
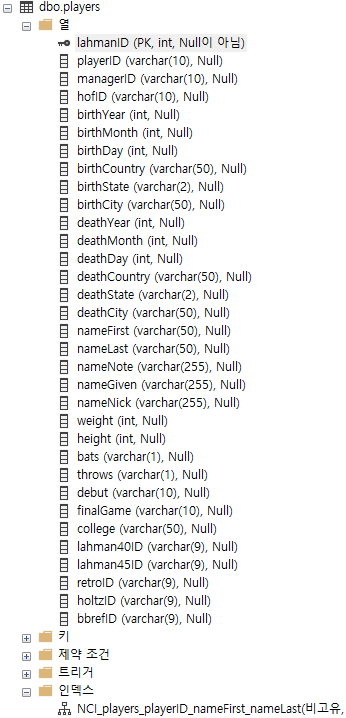
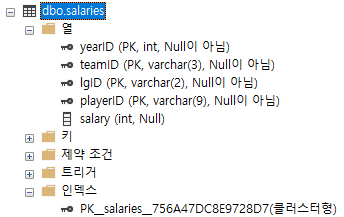
두 테이블을 살펴보면 players는 lahmanId가 프라이머리 키가 걸려 있고, salries는 year, team, lg, player에 걸려 있기 때문에 정렬을 해야하는 것이다. 이렇기 때문에 many-to-many로 진행이 된다.
그렇지만 머지 조인은 one-to-many일 때 가장 빠른데 이를 어떻게 수정해야할까? 바로 outer를 unique 하게끔 설정해야 한다. 따라서 위 SELECT문의 결과가 아쉬운 이유가 many-to-many였기 때문에 이를 one-to-many 조건으로 변경해야 가장 빠른데 그렇지 못한것이다.
따라서 One-To-Many의 상황에서는 outer가 unique해야 하며, 이는 프라이머리키(Pk), unique 키워드를 통해 설정할 수 있다. 이렇게 될 경후 일일히 랜덤 엑세스를 하는 것이 아닌 클러스터드 스캔 후 정렬 하는 판단을 가질 수 있다.
그렇다면 인덱스 스캔이 아닌, 정렬되어 있는 데이터를 사용하면 어떨까? schools과 school player 테이블을 활용해 테스트를 해보자.
-- 데이터 조회
SELECT *
FROM schools AS s
INNER JOIN schoolsplayers AS p
ON s.schoolID = p.schoolID;
위 쿼리의 실행 계획을 보면 정렬을 스킵한 것을 알 수 있다. 그렇지만 schoolsplayers를 스캔할 때 클러스터드 인덱스가 아닌 논 클러스터드 인덱스를 사용하고 있다. 확인해보니 schoolplayers의 테이블의 인덱스를 살펴보면 모든 조건으로 인덱스를 붙인 애가 있어서 논 클러스터드 형태로 진행된 것이다. 이 후 머지 조인의 형태도 many-to-many가 비활성화 된 상태가 된 것을 볼 수 있다.
🐋 결론
Merge 조인은 Sort Mearge 조인으로 알아두자.
1) 양쪽 집합을 Sort(정렬)하고 Merge(병합)한다.
* 이미 정렬된 상태라면 Sort는 생략. 특히 클러스터드로 물리적 정렬된 상태라면 Best이다.
* 정렬할 데이터가 너무 많으면 좋은 상황이 아니며, Hash를 이용하는게 더 나을 수 있다.
2) 랜덤 엑세스 위주로 수행되지 않는다.
3) Many-To-Many 즉. 다대다보다는 One-to-Many(일대다) 조인에 효과적이다.
* PK, UNIQUE가 붙었을 때, 보다 효과적이다.
'공부 > 인프런 - Rookiss' 카테고리의 다른 글
| Part 5-3-10. SQL 튜닝 : Sorting (1) | 2024.07.18 |
|---|---|
| Part 5-3-9. SQL 튜닝 : Hash 조인 (0) | 2024.07.17 |
| Part 5-3-7. SQL 튜닝 : Nested Loop 조인 (0) | 2024.07.15 |
| Part 5-3-6. SQL 튜닝 : 인덱스 컬럼 순서 (1) | 2024.07.12 |
| Part 5-3-5. SQL 튜닝 : 북마크 룩업 (0) | 2024.07.11 |